Are you struggling with geometry and in need of answers to the big math ideas? Look no further! The Big Math Ideas Geometry Answers provide comprehensive solutions to all your geometry problems. From basic concepts to advanced theorems, this resource has got you covered. With clear explanations and step-by-step solutions, understanding geometry has never been easier. Whether you need help with angles, shapes, or proofs, these answers will guide you towards a deeper comprehension of the subject. Visual aids and diagrams are included to enhance your learning experience, making complex concepts more accessible. Whether you’re a student looking to ace your geometry exams or a teacher seeking additional resources for your classroom, the Big Math Ideas Geometry Answers offer the support you need. Say goodbye to confusion and frustration and embark on a journey towards geometry mastery. Don’t let geometry equations and theorems intimidate you anymore; let the Big Math Ideas Geometry Answers be your trusted companion in unlocking the secrets of this fascinating branch of mathematics. Take the first step towards mathematical excellence and explore the world of geometry with confidence.
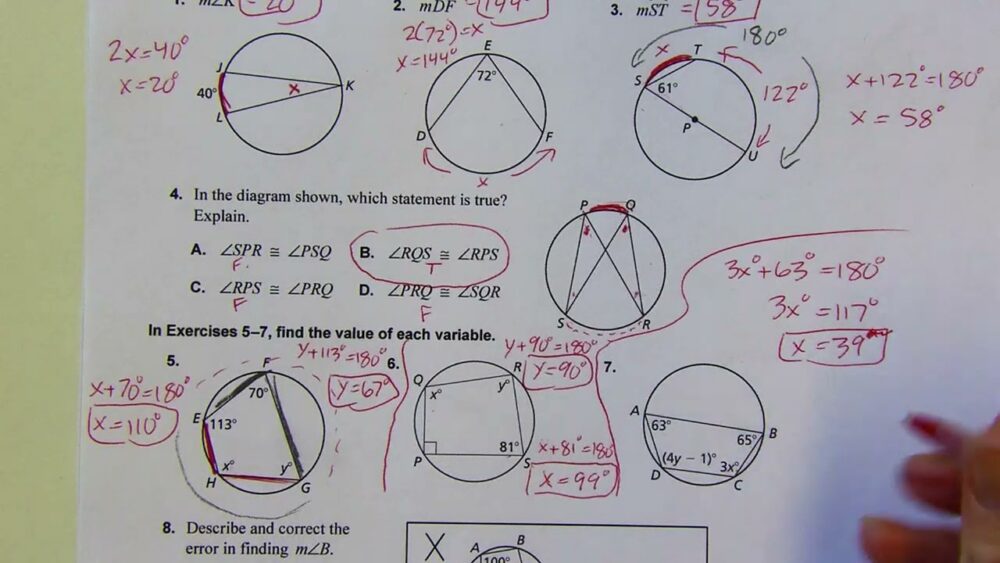
2023 Trending Geometry – Big Ideas – 10.4 Practice
| Topic | Description | Key Concepts |
|---|---|---|
| Euclidean Geometry | Explore the classical branch of geometry that deals with points, lines, and planes. | Postulates, theorems, congruence, similarity, parallel lines, and angle relationships. |
| Coordinate Geometry | Learn how to analyze geometric shapes using algebraic equations and coordinate systems. | Distance formula, midpoint formula, slope-intercept form, equations of lines and circles. |
| Transformational Geometry | Understand how shapes can be manipulated through translations, rotations, reflections, and dilations. | Vector notation, matrix transformations, symmetry, and scaling factors. |
| Trigonometry | Discover the relationship between angles and sides of triangles, and its applications in solving real-world problems. | Trigonometric ratios, Pythagorean theorem, special right triangles, and inverse trigonometric functions. |
| Three-Dimensional Geometry | Explore the properties and measurements of shapes in three-dimensional space. | Surface area, volume, polyhedra, cylinders, cones, and spheres. |
| Non-Euclidean Geometry | Delve into alternative geometries that challenge Euclid’s traditional axioms. | Hyperbolic and elliptic geometries, curved spaces, and non-Euclidean postulates. |
“Unlocking the Secrets of Shape: Dive into Geometry’s Big Ideas through Engaging Practice”
Exploring Big Math Ideas in Geometry
Geometry, the study of shapes and their properties, is an essential branch of mathematics. From ancient civilizations to modern-day advancements, geometry has played a significant role in various fields such as architecture, engineering, and art. In this article, we will delve into five compelling big math ideas in geometry and provide answers to some common questions.
The Pythagorean Theorem: Unlocking the Secrets of Right Triangles
The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is one of the most fundamental concepts in geometry. It states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem, expressed as a^2 + b^2 = c^2, has numerous applications in real-world scenarios, such as calculating distances, determining the lengths of sides, and solving navigation problems.
For example, imagine you want to measure the distance between two points on a map, but there is a river blocking the direct path. By using the Pythagorean Theorem, you can determine the length of a hypothetical bridge needed to connect the two points without having to travel around the river.
Angles: Unraveling the Mysteries of Shape Intersections
Angles are another crucial concept in geometry. They are formed when two lines intersect, and they help us understand the relationship between shapes. Angles are measured in degrees, with a full circle consisting of 360 degrees. There are different types of angles, including acute (<90°), right (90°), obtuse (>90°), and straight (180°).
Angles play a vital role in various applications, such as architecture and engineering. Architects utilize angles to create aesthetically pleasing structures, while engineers use them to design stable and efficient structures. Additionally, angles are essential for understanding the principles of trigonometry, which involves the study of triangles and their properties.
Area and Perimeter: Calculating the Space and Boundaries
Area and perimeter are two fundamental measurements used in geometry to determine the size of shapes and their boundaries. The area refers to the amount of space enclosed within a shape, while the perimeter measures the distance around the shape.
Calculating area and perimeter is crucial in various real-life situations. For instance, when designing a garden, you need to determine the area to know how many plants or seeds to buy. Similarly, when building a fence, knowing the perimeter helps you estimate the required materials.
Transformations: Changing the Shape’s Position and Orientation
Transformations involve changing the position, size, or orientation of a shape without altering its properties. There are several types of transformations, including translation, rotation, reflection, and dilation.
These transformations have practical applications in various fields. For example, in computer graphics, transformations are used to create animated characters or change the orientation of objects in virtual environments. Additionally, transformations are crucial in architecture and engineering, allowing designers to visualize how a building or structure will look from different angles.
Symmetry: Appreciating Balance and Harmony
Symmetry is a fascinating concept in geometry that describes the balance and harmony found in shapes. A shape is symmetrical if it can be divided into two equal parts that mirror each other. Symmetry can be classified into different types, such as reflectional, rotational, and translational symmetry.
Symmetry is prevalent in nature, art, and design. It is often associated with beauty and balance. Architects and artists utilize symmetry to create visually appealing structures and artworks. Furthermore, symmetry plays a crucial role in fields like crystallography and molecular biology, helping scientists understand the properties and behavior of complex structures.
Conclusion
Geometry encompasses a wide range of big math ideas that have significant applications in various fields. From the Pythagorean Theorem to angles, area and perimeter, transformations, and symmetry, these concepts provide us with valuable tools to understand and manipulate shapes.
By exploring these big math ideas in geometry, we can gain a deeper appreciation for the role mathematics plays in our everyday lives. Whether you are an artist, architect, engineer, or simply someone curious about the world around you, geometry offers a fascinating journey into the realm of shapes and their properties.
Big Math Ideas Geometry Answers
#MathMastery #InnovationInLearning