Looking for comprehensive and accurate Big Ideas Math Geometry answers to enhance your understanding of geometric concepts? Look no further! Our meticulously crafted solutions provide in-depth explanations and step-by-step guidance to help you tackle even the most challenging geometry problems. Whether you’re struggling with proofs, angles, congruence, or any other topic in geometry, our answers will unlock the secrets to mastering this fascinating subject. With a focus on conceptual understanding and real-world applications, our solutions go beyond mere calculations, empowering you to truly grasp the underlying principles and build a solid foundation for future mathematical pursuits. Designed to cater to learners of all levels, our Big Ideas Math Geometry answers offer a seamless learning experience, ensuring you can confidently navigate through the intricacies of geometry. No more confusion or frustration – our answers are here to provide clarity and support, allowing you to excel in your geometry studies. So, why wait? Dive into the world of shapes, lines, and angles with our comprehensive Big Ideas Math Geometry answers and witness your geometry skills soar to new heights.
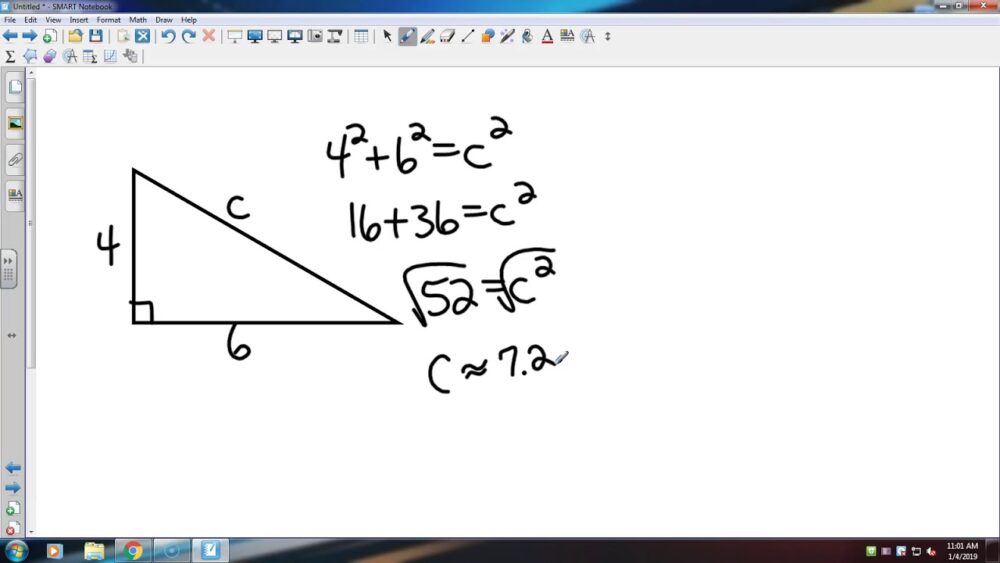
2023 Trending: Big Ideas Geometry 9 1 Pythagorean Theorem
| Concept | Description |
|---|---|
| Pythagorean Theorem | The Pythagorean Theorem is a fundamental concept in geometry that relates to right triangles. It states that in any right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. |
| Applications | The Pythagorean Theorem finds numerous applications in various fields such as architecture, engineering, and physics. It allows us to calculate distances, determine the lengths of unknown sides in right triangles, and solve complex geometric problems. |
| Proofs | There are several elegant proofs of the Pythagorean Theorem, some dating back to ancient civilizations like Ancient Greece and Mesopotamia. These proofs showcase the versatility and beauty of mathematics, providing different perspectives on the theorem’s validity. |
| Converse | The converse of the Pythagorean Theorem is also significant. It states that if the square of the length of the hypotenuse of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle. This converse allows us to determine if a triangle is right-angled using the theorem. |
| Extensions | The Pythagorean Theorem has led to the development of more advanced concepts in geometry, such as the Law of Cosines and the Law of Sines. These extensions provide valuable tools for solving non-right triangles and further exploring the relationships between their sides and angles. |
“The Pythagorean Playground: Unleashing the Power of the Triangle”
Big Ideas Math Geometry Answers: Unlocking the Secrets of Geometry
Geometry, the branch of mathematics that deals with the properties and relationships of points, lines, angles, surfaces, and solids, is a fundamental subject that holds immense importance in various fields such as engineering, architecture, and physics. However, understanding the complex concepts and solving intricate problems in geometry can be challenging for many students. This is where Big Ideas Math Geometry Answers come into play. In this article, we will explore the significance of Big Ideas Math Geometry Answers and how they can help students overcome the hurdles of geometry.
1. What are Big Ideas Math Geometry Answers?
Big Ideas Math Geometry Answers serve as a comprehensive guide for students to check their solutions and verify their understanding of geometry problems. These answers provide step-by-step explanations, allowing students to follow along and grasp the concepts more effectively. By having access to Big Ideas Math Geometry Answers, students can compare their own solutions with the correct ones, identify any mistakes they may have made, and learn from them.
2. Benefits of Using Big Ideas Math Geometry Answers
Using Big Ideas Math Geometry Answers offers numerous benefits for students:
1. Enhanced Understanding: When students have access to the correct answers, they can compare their own solutions and identify any gaps in their understanding. By analyzing the step-by-step explanations provided in the answers, students can gain a deeper comprehension of the underlying concepts.
2. Practice and Reinforcement: Big Ideas Math Geometry Answers allow students to practice solving a wide range of geometry problems. This repetitive practice helps reinforce their understanding and build confidence in their problem-solving skills.
3. Immediate Feedback: With Big Ideas Math Geometry Answers, students no longer have to wait for their teachers to grade their assignments. They can obtain immediate feedback on their solutions, enabling them to make corrections and improve their performance in a timely manner.
3. How to Use Big Ideas Math Geometry Answers Effectively
While Big Ideas Math Geometry Answers are undoubtedly helpful, it is crucial for students to use them effectively to maximize their benefits. Here are a few tips:
1. Solve Problems Independently: Before referring to the answers, attempt to solve the geometry problems independently. This will help you gauge your own understanding and identify areas that need improvement.
2. Compare Solutions: Once you have solved a problem, compare your solution with the Big Ideas Math Geometry Answers. Analyze the differences and try to understand the reasoning behind the correct answer. This will enhance your understanding of the concepts.
3. Learn from Mistakes: If your solution differs from the correct answer, carefully examine your mistakes. Understand where you went wrong and why. This process of self-correction will help you learn from your errors and avoid making similar mistakes in the future.
4. Supplementing Classroom Learning
Big Ideas Math Geometry Answers can be an excellent supplement to classroom learning. While teachers provide instruction and guidance during class, having access to the answers allows students to reinforce their learning independently. They can practice more problems, explore alternative solution methods, and deepen their understanding of geometry beyond what is covered in the classroom.
5. Utilizing Online Resources
In addition to Big Ideas Math Geometry Answers, there are numerous online resources available to further enhance your geometry skills. Online tutorials, interactive quizzes, and video lessons provide additional support and practice opportunities. These resources, combined with the guidance of Big Ideas Math Geometry Answers, can help you become a proficient geometry problem solver.
In conclusion, Big Ideas Math Geometry Answers play a crucial role in helping students navigate the complexities of geometry. By providing step-by-step explanations and allowing students to compare their solutions, these answers enhance understanding, reinforce learning, and provide immediate feedback. Remember to use Big Ideas Math Geometry Answers effectively, supplement them with classroom learning, and explore additional online resources to become a geometry master!
Big Ideas Math Geometry Answers
#CreativeMath #MathRevolution