The Big Math Ideas Geometry Answers: Are you struggling to grasp the concepts of geometry? Look no further! Our comprehensive resource offers clear and concise solutions to all your geometry problems. Whether you’re a student, teacher, or simply an avid learner, our answer key provides a deep understanding of the big ideas in geometry. Triangles, angles, and circles will no longer be a mystery to you. With step-by-step explanations and diagrams, you’ll gain confidence in tackling even the most challenging geometric puzzles. Our carefully crafted answers are designed to enhance your problem-solving skills and expand your geometric knowledge. Unlock the secrets of geometric theorems and proofs, and discover the beauty and elegance of this mathematical discipline. Whether you’re preparing for an exam or simply seeking to deepen your understanding, our geometry answers will guide you on your path to success. So, why struggle with geometry when you can access comprehensive answers that make learning enjoyable and efficient? Dive into the world of geometry today and watch your mathematical skills soar to new heights!

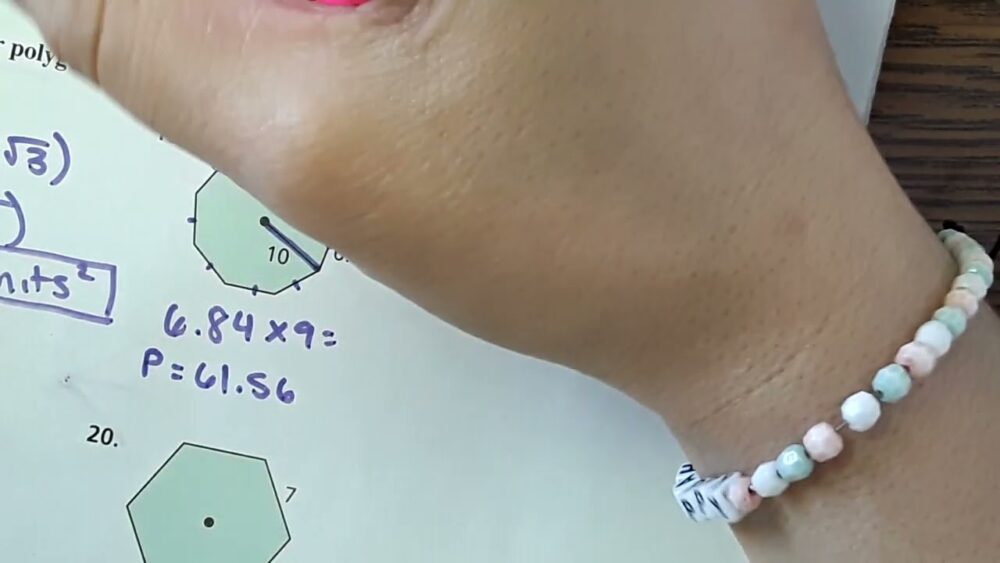
2023 Trending Geometry Lesson 11.3: Areas of Polygons
| Polygon | Formula | Example | Interesting Fact |
|---|---|---|---|
| Triangle | A = 1/2 * base * height | A = 1/2 * 7 * 4 = 14 | Triangles are the simplest polygon, and their area calculation is straightforward. |
| Rectangle | A = length * width | A = 5 * 10 = 50 | Rectangles are quadrilaterals with equal opposite sides and right angles. |
| Square | A = side^2 | A = 6^2 = 36 | Squares are special rectangles where all sides are equal in length. |
| Parallelogram | A = base * height | A = 8 * 3 = 24 | Parallelograms have opposite sides that are parallel and congruent. |
| Trapezoid | A = 1/2 * (base1 + base2) * height | A = 1/2 * (6 + 9) * 5 = 37.5 | Trapezoids have one pair of parallel sides and can have different side lengths. |
| Pentagon | A = 1/2 * apothem * perimeter | A = 1/2 * 4 * (2 + 3 + 4 + 5 + 6) = 35 | Pentagons are five-sided polygons with equal internal angles. |
“Unleashing the Power of Polygonal Spaces: Mastering Area Calculations in Geometry Lesson 11.3”
The Power of Geometry Answers: Unraveling Big Math Ideas
Geometry, one of the oldest branches of mathematics, has fascinated scholars and thinkers for centuries. From ancient civilizations to modern classrooms, the study of shapes, sizes, and spatial relationships has provided a framework for understanding the world around us. In this article, we will explore some big math ideas in geometry and delve into their significance in various fields.
The Pythagorean Theorem: Unlocking the Secrets of Right Triangles
The Pythagorean Theorem, named after the Greek mathematician Pythagoras, is a fundamental concept in geometry. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This simple equation, a² + b² = c², has far-reaching implications in fields as diverse as architecture, physics, and navigation.
Architects rely on the Pythagorean Theorem to ensure that buildings are structurally sound. By applying this theorem, they can calculate the lengths of diagonal supports and determine the angles and dimensions required for stability. Similarly, physicists use this theorem to analyze forces and motion, enabling them to predict the behavior of objects in space.
Fractals: Nature’s Infinite Patterns
Fractals are intricate mathematical patterns that repeat themselves infinitely at different scales. These mesmerizing shapes can be found in nature, ranging from the branching patterns of trees to the intricate designs of snowflakes. Fractals have captivated mathematicians, artists, and scientists alike, offering a glimpse into the inherent beauty and complexity of the universe.
One of the most famous fractals is the Mandelbrot set, named after the mathematician Benoit Mandelbrot. This set is generated by a simple mathematical equation, yet its infinite complexity and self-similarity have astounded researchers. Fractals have applications in computer graphics, where they are used to create realistic landscapes, textures, and animations. They also have implications in fields such as biology, where they can model the growth of organisms and the distribution of resources.
Transformations: Shaping the World Around Us
Transformations, such as translations, rotations, reflections, and dilations, allow us to manipulate and understand the properties of shapes. They provide a powerful toolset for architects, graphic designers, and engineers, enabling them to create, modify, and analyze complex structures and designs.
Translations, for example, involve moving an object without altering its shape or orientation. This concept is crucial in architecture, as it allows architects to position buildings accurately on a plot of land. Rotations, on the other hand, involve turning an object around a fixed point. This concept is essential in fields such as manufacturing, where engineers need to rotate objects to reach specific angles during production.
Non-Euclidean Geometry: Expanding the Boundaries of Thought
For centuries, Euclidean geometry, developed by the ancient Greek mathematician Euclid, was considered the only valid form of geometry. However, in the 19th century, mathematicians discovered the existence of non-Euclidean geometries, which challenged long-held assumptions and opened new avenues of exploration.
Non-Euclidean geometries, such as hyperbolic and elliptic geometries, exhibit properties that differ from those of Euclidean geometry. These geometries have found applications in various fields, including physics, computer science, and cosmology. Einstein’s theory of general relativity, for instance, relies on non-Euclidean geometries to describe the curvature of spacetime.
The Beauty of Symmetry: Exploring Reflections and Rotations
Symmetry, a fundamental concept in geometry, is deeply ingrained in our perception of aesthetics and harmony. From the intricate patterns of a snowflake to the grandeur of a cathedral, symmetry is all around us, captivating our minds and stirring our emotions.
Reflection symmetry, also known as bilateral symmetry, occurs when an object can be divided into two equal halves that are mirror images of each other. This type of symmetry is prevalent in nature, from the wings of butterflies to the faces of humans. Rotational symmetry, on the other hand, occurs when an object can be turned around a fixed point and still appear the same. This type of symmetry is often seen in flowers and other natural forms.
In conclusion, geometry answers provide us with a powerful framework for understanding the world. From the Pythagorean Theorem to fractals, transformations, non-Euclidean geometries, and symmetry, these big math ideas have shaped our understanding of the physical and abstract realms. Whether we are designing buildings, exploring the cosmos, or appreciating the beauty of nature, geometry continues to inspire and illuminate our path.
Big Math Ideas: Geometry Answers
#Mathematics #Education #GeometricConcepts #MathLessons #PolygonAreas #KeyConcepts